Research Thrusts
Computational Biomechanics (Bone & Cell Mechanics)
Computational Methods (Meshfree & Cohesive Zone Methods)
Computational Material Failure Analysis
Bioinspired Design of Hybrid Nanocomposites
Ferroelectric Materials Modeling and Simulation
Multiscale Modeling and Simulation
Nanomechanics and Microcontinuum Theory
Bone Mechanics
Modeling and Simulation of Osteoporosis in Trabecular Bone
Osteoporosis is a skeletal disease characterized by a decrease in bone strength as a result of a decrease of bone mass and a deterioration of bone microstructure. In this study, the imaging data of a CT scanned human femoral neck trabecular bone is directly converted into a meshless model. A model is developed to analyze osteoporosis process. A fracture criterion and the corresponding post-failure are proposed for trabecular bone. The fracture process is modeled and simulated. The simulations show that the fracture stress is not a monotonically decreasing function in the process of fracture, and the microstructure of trabecular bone has a positive effect in preventing progressive failure.

The 3D meshless model, from left to right: stage 1, stage 2 and stage 3
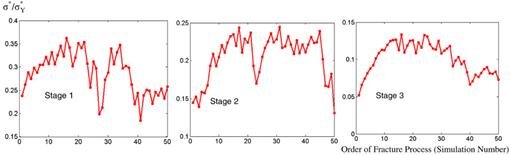
Normalized fracture stress in fracture process
Fracture of Extrafibril Matrix in Bone
Bone poses various levels of hierarchical structural organization from macroscale to nanoscale.The mechanism of bone failure has been extensively studied, however, the underlying mechanism of plastic deformation in bone is still a debating issue. The possible pathways for plastic flow in bone are most likely due to the sliding between mineral cyrstals, between mineral and collagen phases, or between the mineralized collagen fibrils. At ultrascale level, the extrafibrillar matrix in bone consists of hydroxyapatite (HA) polycrystals bounded through an organic interface (grain boundary).
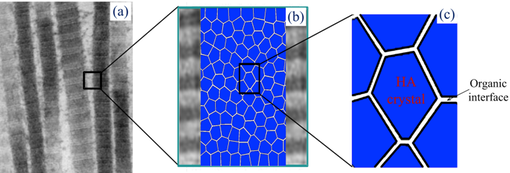
Schematic representation of ultrastructure of extrafibrillar matrix in bone
Deformation process of extrafibrillar matrix under compression
Cell Mechanics
Cell Adhesion and Spreading
Recently, we have developed a multiscale soft matter model for stem cells or primitive cells in general, aiming at improving the understanding of mechanotransduction mechanism of cells that is responsible for information exchange between cells and their extracellular environment. In this study, we report the preliminary results of our research on multiscale modeling and simulation of soft contact and adhesion of cells. The proposed multiscale soft matter cell model may be used to model soft contact and adhesion between cells and their extracellular substrates. By using the soft matter cell model, we have simulated the soft adhesive contact process between cells and their extracellular substrates. The simulation shows that the cell can sense substrate elasticity by responding in different manners from cell spreading motion to cell contact configurations.
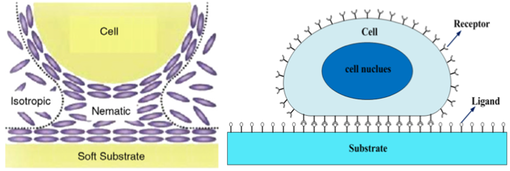
Soft matter cell model and adhesive contact model
Cell-substrate adhesion (2D)
Cell spreading (Axisym)
Cell spreading (3D)
Collective Epithelial Cell Migration
Cell migration is a fundamental biological process throughout all the stage of animal life, from its commencement to its end. A variety of complex mechanisms, such as embryonic morphogenesis and wound healing, in development, health and disease depend on the coordinated motion of cell groups. Some cells migrate as individuals, but many cell types will migrate collectively in tightly or loosely associated groups under physiological conditions. Although factors affecting migration of single cell are beginning to be understood, still little is known about motion when cells are in collective groups. To explore the migration behavior of collective cells, the collective epithelial cell migration was studied.
Collective migration of an epithelial monolayer sheet
Epithelial Cell Growth and Division
Most of the cell proliferation is in the epithelial tissue and around 80% of human cancers progress at epithelial sheets , which results in a popularity of research into epithelial tissue. In epithelial tissues, cells are packed together closely , which is different from cell dispersion in connecting tissue. The behavior of cell ensembles is widely studied by the cell-based models, such as epithelial mono-layers , multi-cell spheroids, and Dictyostelium discoideum slug. Epithelial cell behavior has been studied widely, very little is known about the possible implications of cell pattern geometry for mechanical properties of tissues or key biological processes, such as planar polarization, cell division and tissue remodeling. Thus, cell division and cell-cell interactions also lead to a great deal of interest.
Epithelial cell division process in a restricted lattice-based box
Material Failure Analysis
Failures can occur for many reasons in engineering structures. They include uncertainties in the loading or environment, defects in the materials, inadequacies in design, and deficiencies in construction or maintenance. Large scale destruction has been witnessed in wide ranges of applications involving aeronautics, automobiles, bridges and highways, and great loss has been induced in human life and economics. These disasters may have occurred due to some pre-existing crack or a defect during the production or during service.
Crack propagation
Crack nucleation, growth and coalescence
High-speed impact induced spall fracture
High-speed impact induced spall fracture in composite materials
Intergranular fracture in polycrystalline Al2O3
Transgranular fracture in polycrystalline Al2O3
High-speed impact induced spall fracture in polycrystalline materials
Multiscale Modeling and Simulation
Both atomistic simulations and classical continuum theories have their limitations, i.e., atomistic simulations can be accurate, but are inefficient and impractical for large systems and long time-scales even with latest computing power; similarly continuum theories are efficient for large systems, however, they are inaccurate for miniaturized devices with atomistic features, major challenges exist for simulating micro/nano-scale systems over a realistic range of time, length, and temperature. So, different multiscale methods have been developed and it bridges various lengths and time scales are central for further advances in micro/nano-scale systems.
Atomistic Simulation
BCC to FCC phase transformation in Fe (Tension)
Dislocation evolution & finite size effects (Compression)
Crack propagation
Coarse-Grained MD
Uniform compression
Simple tension
Multiscale Modeling
Simple tension
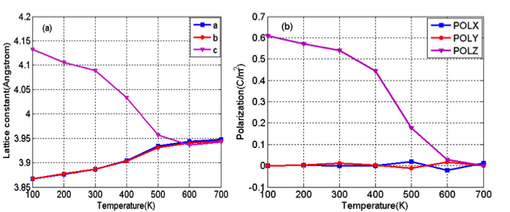
Ferroelectric Material Modeling and Simulation
Based on a shell model potential obtained from first principles calculations, the molecular dynamics simulations were performed to investigate the electromechanical response of a ferroelectricperovskite under finite temperature and electric field. We characterize the switching paths by which a homogeneous polarization reorientation process would take place in the prototypical ferroelectric PbTiO3.
Cubic to tetragonal phase transformation
Polarization switching
Microcontinuum Theory
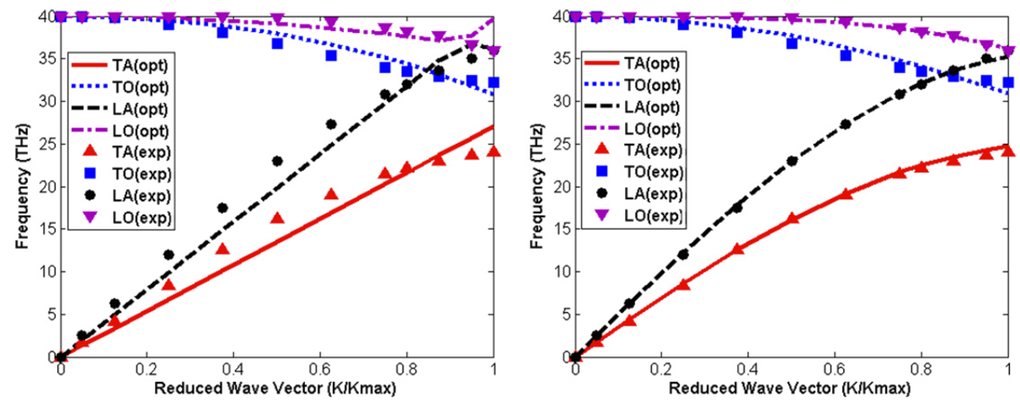
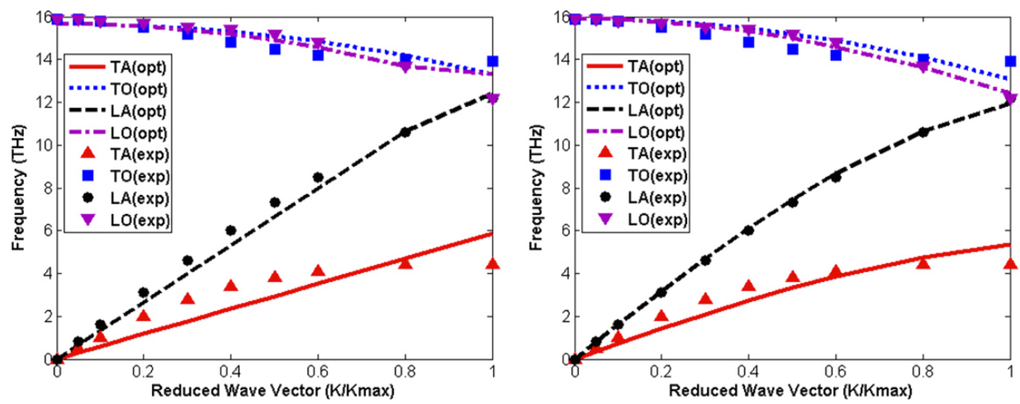
Micromorphic theory describes both acoustic and optical vibrations. This dramatically extends the application region to a time scale in accordance with lattice dynamics. However, the phonon dispersion relations from experimental measurements and local micromorphic theory can only match well in half of the Brillouin zone, while the matching for the entire Brillouin zone is quite off. When the micromorphic theory is incorporated with the nonlocal theory, the phonon dispersion relations from experimental measurements and from the nonlocal theory match almost perfectly for diamond and quite well for silicon. The nonlocal micromorphic theory thus extends the wavelength region down to scales that lattice dynamics applies. It is therefore believed that the nonlocal micromorphic theory has the great promise and enough accuracy in describing those coupling effects between mechanical, EM and optical behaviors of crystals and extend its application region from microscopic to nanoscopic length scales.
Phonon dispersion relations of dimond calculated by local micromorphic theory (left) and nonlocal micromorphic theory (right) with fitting in whole BZ
Phonon dispersion relations of silicon calculated by local micromorphic theory (left) and nonlocal micromorphic theory (right) with fitting in whole BZ