The operation of a power system entails solving problems on significantly different time-scales ranging from a time-horizon of years for distributed generation and power system planning, to daily/hourly unit commitment and economic dispatch problems, to milliseconds for frequency and voltage regulation.
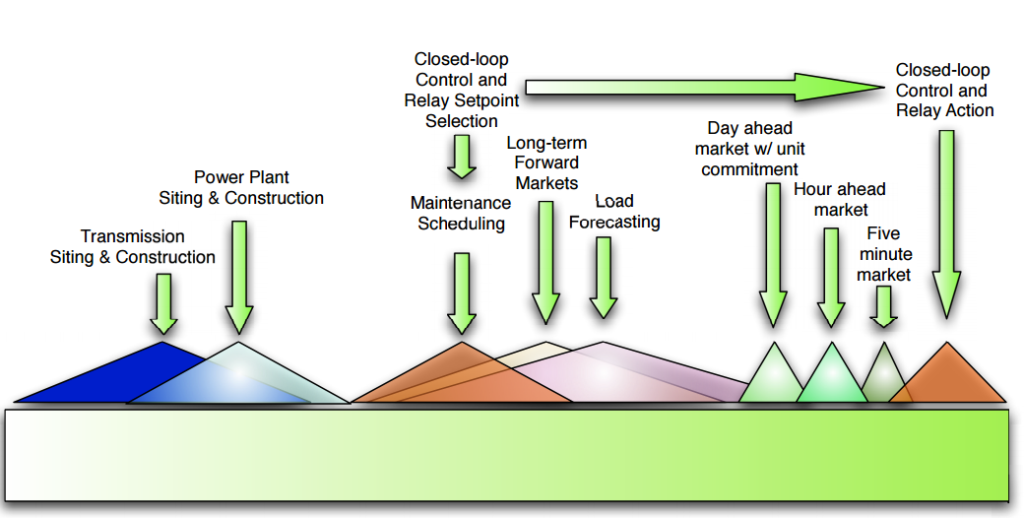
Examples of Coupling Operation and Stability Control Time-Scales
The above figure depicts the idea of extreme time-scales encountered in power systems applications. For example, transmission expansion, installation of generators, and getting approvals to build power plants are all considered to be planning optimization problems—with time-spans ranging from years to decades—where the variables are often integers and the problems are modeled as mixed integer optimization problems. Other decision-making problems encompassed in smart grids are depicted the above figure.
There are many examples in power systems in which steady-state and transient operation of power systems are physically coupled. For example, economic dispatch decisions influence the problem of procuring automatic generation control and energy storage can provide load-shifting on slow timescales and frequency regulation on fast timescales. In this case, the storage decisions must jointly respect physical limitations such as power and capacity limits.
Proposed Approach
For decades, these problems have traditionally been treated separately—for simplicity and ease of analysis. With the integration of renewables, the time-scales separation shrinks. Our recent work in this topic aims to integrate two crucial power network problems with different time-scales. The first problem is the steady-state optimal power flow (OPF), whose decisions are updated every few minutes.
The second is the problem of load-following stability that spans the time-scale of several seconds to one minute. Specifically, the OPF problem is augmented to account for the costs associated with the load-following stability of a power network described by a set of nonlinear, uncertain differential algebraic equations (DAEs). The developed approach, scalable to networks with thousands of nodes, yields new OPF operating points that show much improved overall system costs and significant reductions in the frequency oscillations.
The below figure shows the performance of the new operating point and the LQR-based control algorithm of a power network with ten generators (case39 from MATPOWER).
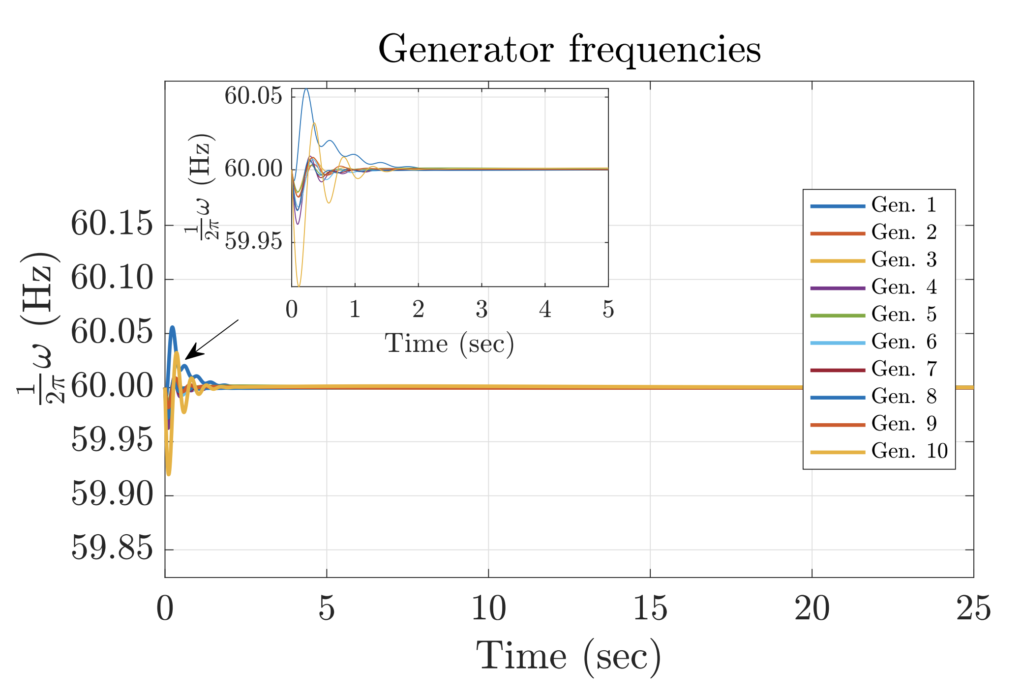
The below figure shows the performance of the same power network under a scenario where the OPF is solved independently on the load-following constraints. The two figures simply show that new operating points (i.e., generator setpoints) can be derived without encumbering additional operational costs, while significantly leading to reduction in frequency deviation after a heavy load or distributed generation disturbances.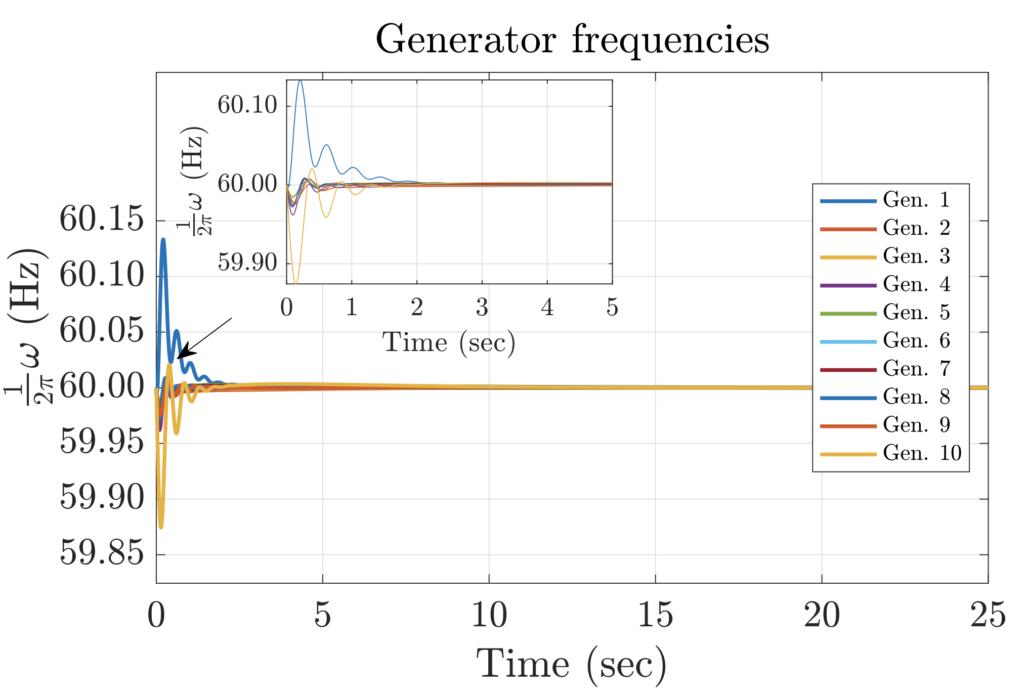
Interested in learning more? Please have a look here for the technical details and here for the Github codes.

