Thousands? Millions? Or Billions? How many sensors and actuators (SaA) do basic infrastructures such as transportation networks, water distribution networks, and smart grids all have? The answer is dazzling!
These infrastructures have hundred of billions in SaAs between them. In fact, IBM predicts that we’ll have trillions of IoT/CPS SaAs by 2020. As our smart connected communities are becoming smarter and more integrated, while embedding cheap, ubiquitous SaAs, more operations can be simultaneously performed to achieve superior system-level performance. For example, reducing energy consumption in energy systems, minimizing traffic in transportation networks, and decreasing contamination in drink water networks, can all become objectives that can be satisfied. The collective wisdom of interacting devices and subsystems in CPSs can lead to flourishing welfare. The question that begs itself—the same question that tech companies crave to answer—is how can data (sensors) and controls (actuators) be used to ultimately improve the user experience, societal interactions, and reliability.

Why do we need dynamic selection of SaAs?
IoTs and CPSs face the same dilemma: how can a system operator dynamically utilize the sheer amount of SaAs? How can we cherry-pick omnipresent SaAs in CPSs that are evolving in their topology?
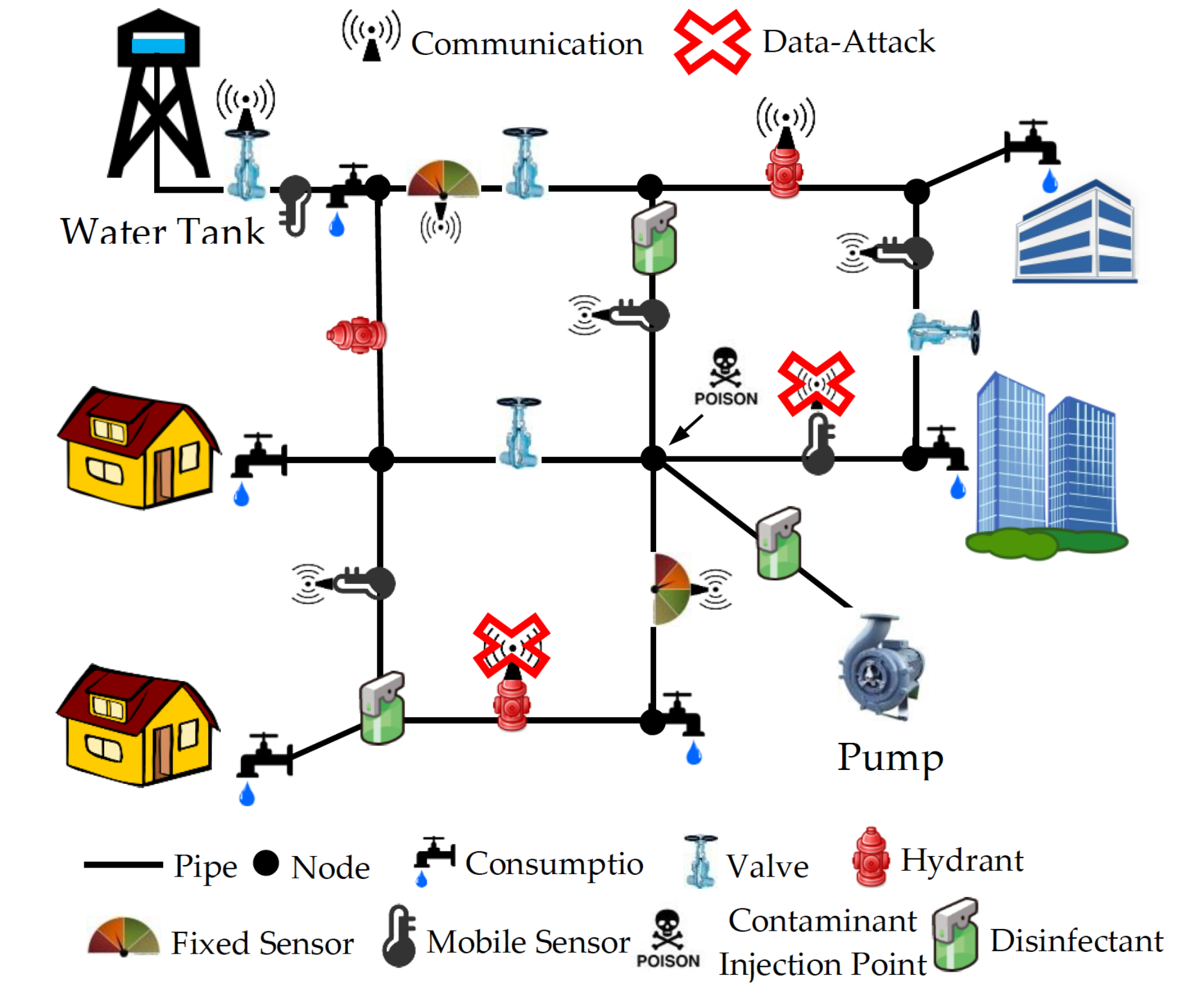
As sampling data from billions of sensors and sending control actions to millions of actuators are not a feasible approach, intelligent selection of SaAs becomes a research question of great importance and resounding implications. Why is that important, though? The following questions answers this question. Could the water-contamination disaster have been avoided in Flint, Michigan had the city planners placed sensors that detected the contamination levels from lead, and subsequently opened some water valves to mitigate that? Can transportation networks operate with traffic lights that change in real-time? Can they operate without traffic lights? Would it be possible for large cities to manage their energy consumption, while maximizing renewable energy penetration through dynamic selection of SaAs? While research results speculates that this is a possibility, there is a lack—some might say absence—of scientific frameworks that can guide the process of dynamic selection of SaAs in CPSs that are constantly evolving.
Model Details
We model uncertain CPSs as follows:
(1) 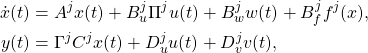
where ![]() are the CPS’s states, control inputs, sensor measurements, unknown inputs, and potential sensor noise and/or data attacks;
are the CPS’s states, control inputs, sensor measurements, unknown inputs, and potential sensor noise and/or data attacks; ![]() denotes the time-period which changes at a slower pace than the CPS’s transient behavior;
denotes the time-period which changes at a slower pace than the CPS’s transient behavior; ![]() denotes a vector of time-varying nonlinearities; matrices
denotes a vector of time-varying nonlinearities; matrices ![]() are all given (and a function of the CPS’s topology and parameters);
are all given (and a function of the CPS’s topology and parameters); ![]() and
and ![]() are block-diagonal matrices that cherry-pick the specific sensors and actuators—these matrices are considered as binary variables, with
are block-diagonal matrices that cherry-pick the specific sensors and actuators—these matrices are considered as binary variables, with ![]() implying that the
implying that the ![]() th actuator is activated.
th actuator is activated.
The high-level problem for time-varying SaA selection can be formulated as follows:
(2) 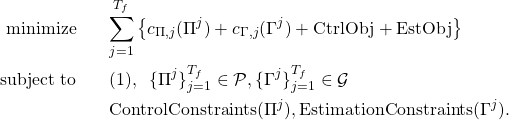
In (2), the objective is to minimize the sum of the cost as a function of the selected SaAs and certain control and estimation metrics which can vary depending on the metric to be studied. The constraints include the dynamical system evolution for all time-periods ![]() , and operational set constrains (
, and operational set constrains (![]() and
and ![]() ) on
) on ![]() and
and ![]() that include the binary nature of these variables and possibly ramp constraints as a function of previous SaA selection. The control and estimation constraints depend on the considered estimation and control metrics.
that include the binary nature of these variables and possibly ramp constraints as a function of previous SaA selection. The control and estimation constraints depend on the considered estimation and control metrics.
Thousands of SDP Formulations
The common instrument we use in this work is semidefinite programs (SDP). Thousands of various control/estimation problems can be posed as convex optimization problems and SDP or linear matrix inequalities. Given this advantage, the simultaneous problems of SaA selection and the corresponding design of controllers and estimators can be studied. Boyd et al.’s book is a perfect on example on the prevalence and extensiveness of SDP formulations in controller/observer design problems, which can be extended to the context of SaA selection problem.
Our Approach
We propose methods to solve time-varying, sensor and actuator (SaA) selection problems for uncertain cyber-physical systems. We show that many SaA selection problems for optimizing a variety of control and estimation metrics can be posed as semidefinite optimization problems with mixed-integer bilinear matrix inequalities (MIBMIs). Although this class of optimization problems is computationally challenging, we present tractable approaches that directly tackle MIBMIs while providing both upper and lower bounds and lead to effective heuristics for SaA selection. The upper and lower bounds are obtained via successive convex approximations and semidefinite programming relaxations, respectively, and selections are obtained with a novel slicing algorithm from the solutions of the bounding problems. Custom branch-and-bound and combinatorial greedy approaches are also developed for a broad class of systems for comparison. The interested reader is encouraged to check a draft of this work here.